Quantum Cryptography: Enabling Secure Data Transmission

Traditional cryptographic methodologies rely on mathematics and have theoretical limits on computational power. There are different mathematical tricks and techniques that facilitate the factorisation of extremely large numbers into their corresponding primes, hence making cryptanalysis—the study of finding security vulnerabilities in cryptographic systems—a popular and achievable task. The RSA has done reasonably well over the last two decades and remains most popular yet resilient to hackers. Named after its three inventors, Rivest, Shamir and Adleman, according to Wikipedia, it is one of the first practicable public-key cryptosystems and is widely used for secure data transmission. Factoring a modulus is referred to as a brute-force attack in the case of RSA. The most efficient factoring algorithm is general number field sieve (GNFS), that runs in , for ‘’n bit’’ integer; where c<2. Though GNFS is far from polynomial bounds and in current state doesn’t possess much threat to RSA. Several planned attacks to exploit its mathematical aspects are possible—like low exponent (both private and public), blinding, chosen cipher text, cycle attacks, etc. The computational power of electronic devices is increasing day by day, with even Moore’s law approaching obsolescence. Moreover, the onset of research and development on quantum computing makes current cryptographic methods prone to cryptanalysis.

Quantum cryptography takes encryption and decryption to a different level. It brings physics into action rather than relying too much on mathematical computations and assumptions. The US government backed DARPA’s (Defense Advanced Research Projects Agency) quantum network is the world’s first fully functional quantum cryptographic network running between DARPA, Harvard University and Boston University. Let us now take a ride on quantum mechanics.

Perception and simulation
Qubit: The basis of quantum cryptography is a qubit (a quantum bit). The term ‘quantum’ is derived from the word quanta, which means a packet of energy. This packet contains photons, and these photons constitute a qubit. Thus, quantum computing and quantum cryptography are based on the properties and the characteristics of these photons. In digital signal processing, a bit represents the state of 0 or 1 at a particular instant; quantum annealing defines a bit in three states of 0, 1 and in superposition state (simultaneous occurrence or orientation of both 0 and 1). The states of the qubit are represented in terms of probabilistic amplitudes, though different representations of the qubit are adopted by various research firms, the most common and standard being the ‘ket representation’, 0 as |0> and 1 as |1>. In general, the state of a qubit is defined on the complex plane by the equation: |q> = a|0> + ß|0, where |a|2 + |ß|2 = 1 and are called the amplitudes. The probability of the occurrence of |0> is |a|2 and of |1> is |ß|2. The set of all possible orientations of |q> is plotted on Hilbert’s space (a complex unit circle). Often, a different geometrical representation (Bloch sphere) is done for qubits that have pure states or a two level quantum state. Discussing  Hilbert’s space and Bloch sphere is beyond the scope of this article, so interested readers can contact the author via email. Figure 1 shows a normal bit plot and Figure 2 shows a qubit plot.

Measurement of a qubit: Entanglement is a property specifically related to quantum mechanics, which increases the degree of co-relation among qubits. According to this property, if the quantum state of one qubit is known, then the quantum state of the other qubits in the same reference frame can be found. For example, in a hypothetical reference frame, if there are two qubits and if we know that one qubit is spinning clockwise, then due to analogous behaviour, the other qubit must spin in the anticlockwise direction. The latter qubit is called the mate of the former. Due to entanglement, qubits achieve inherent parallelism.

As discussed before, qubits are the abstraction of photons with their control devices, and due to their potential to incorporate multiple states simultaneously, they are capable of processing millions of computations in a single instant. A single qubit, due to its superposition, is capable of carrying the two states, 0 and 1, in a single instant; hence, what two traditional bits can do is done by a single qubit. A 300 qubit quantum computer can process 2300 computations in an instant (more than the number of atoms in the known universe).

Quantum channel
Researchers are often confused over the paradox of dual transmission – encoding via qubits and transmitting encoded information with traditional bits over classical networking. Our communication channels follow laws and constraints of classical physics. Quantum mechanics out-performs these native laws and leads to the emergence of quantum channels. A property related to quantum mechanics, called ‘no-cloning’, states that we cannot clone (construct) an identical copy of the state (spin, orientation or polarisation) of an unknown qubit. The no-cloning property can be considered as a lemma to the ‘Uncertainty Principle’ of quantum mechanics, which formulates the precision inequality in signal processing. Thus, for a hypothetical situation of Alice and Bob, Bob cannot fully decode what Alice had encoded using qubits and dispatched using traditional bits via a classical channel. Even if Bob is aware of the qubit state (a less secure version, only fit for theoretical understanding), the classical channel needs to carry an infinite number of traditional bits so as to fully decode the information encrypted via qubits (as discussed above, a single qubit can have two states, resulting in 2x possibilities). Due to these limitations, our current networking media must be replaced by quantum networking to facilitate quantum mechanics in our day-to-day life.

Quantum cryptography
Quantum tips and techniques provide far more secure methodologies for various cryptographic tasks facilitating quantum information theory. Under current commercial communication systems, it is primarily government bodies and a few high-end security companies that are interested in quantum cryptographic techniques. A few firms have started providing networking solutions formulated on quantum mechanics—for example, Swiss Quantum, MagiQ, etc.

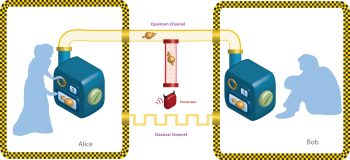
One of the most fundamental aspects of any cryptographic system is the key distribution between sender and receiver. Quantum Key Distribution (QKD) is one of the most well established aspects of cryptography, governed by the laws of physics. In our quantum channel, the sender is Alice and the receiver is Bob. Now, as we have seen earlier, qubits follow the ‘no-cloning’ principle. So, if any eavesdropper tries to grasp the state of the qubit (i.e., polarisation) during the secret key exchange between Alice and Bob, the victim qubit is destroyed (either its polarisation, spin or both) and, hence, the eavesdropper is unable to decode the qubit. Bob gets a qubit with a failed checksum (a protocol to check data integrity) and asks Alice for retransmission. Thus, the only overhead is the retransmission of the victim qubit by Alice.

In 1984, Charles Bennett and Gilles Brassarad (BB84) formulated a protocol for quantum key distribution. It assumes a quantum channel for key distribution and classical channel for data transmission. The process starts with Alice choosing two strings, X and Y, and then encoding them with qubits. Let us now define a term called basis, which is a vector that defines a coordinate system; mathematically, this is a set of linearly independent vectors over a real or a complex plane. Hence, if a vector V {v1, v2, …… vn} is finite and X {x1, x2, ….. xn} denotes coordinates of vector X, then according to this principle, V forms the basis of X if the following two conditions hold:

• If x1v1 + x2v2 + x3v3 +… … … +xnvn = 0 then x1 = x2 = x3 = … … … = xn = 0
• For all ‘x’ in X, x = x1v1 + x2v2 + x3v3 +… … … +xnvn where xi is called the coordinate of vector X with respect to basis V.

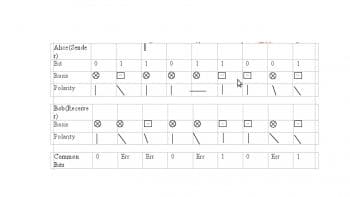
In our key distribution, the ith bit of Y decides the basis of the ith bit of X. Since each bit of X is encoded using the basis of Y, it is practically impossible to decode X without knowing Y. Now, Alice transfers X to Bob over the quantum channel. During this transfer, an eavesdropper, say Eve, might try to obtain a state of X. At this point, three states of X co-exist, one each with Alice, Bob and Eve, while only Alice knows the basis Y. Both Bob and Eve predict their own version of Y, say B and E. Using their respective basis, Bob and Eve begin generating their own version (or state) of X. Now, Bob broadcasts to Alice, acknowledging his version of X calculated using basis B, say X’. Alice and Bob now begin checking or comparing each bit of X and X’. The bits where X and X’ are not equal are discarded. Of all the n bits in X, let m bits match with X’. There is always a lower limit on matching bits, below which the current vector X and its basis Y are discarded, and Alice repeats the whole process again. Alice chooses a random number of bits from among the matched bits (usually m/2) and declares it as a shared key. During this process of bit matching and declaration, Alice and Bob use another property of analytical physics called privacy amplification, which measures differences in amplitude of the signals transferred from Alice to Bob and vice versa. Any difference in amplitude means suspicious behaviour (eavesdropper) in the channel, and hence a hand break is performed and the whole process is started again. If, at any instant, Eve using her own basis E, tries to replicate bits that are acknowledged between Alice and Bob, these bits change their spin, polarity or both at that very instant due to the no-cloning theorem; hence, Alice performs a hand break with Bob and repeats the whole process by selecting a new X and Y, and then retransmits. Figure 4 shows a hypothetical example of qubit matching.

Hence, the agreed key between Alice and Bob in the above example is: 00101. As seen in the table in Figure 4, this protocol has single orientation and polarity for a bit. Therefore, the single photon source is used. Practically, a single photon is difficult to emerge, as photons exist in packets (quanta). Several other algorithms have been developed on the basis of BB84, which exploit the collective pattern and behaviour of photons and are under constant improvement. Some algorithms take advantage of the inherent co-relation of the polarity of photons (entanglement); such algorithms make a guess of bit orientation at Bob’s end, knowing its orientation at Alice’s end. Again, in such cases, the probability of eavesdropping or counterfeiting is nullified by the no-cloning property of the photons.

Similar to the process of key distribution, data encoded with qubits can be transferred. One major drawback in data transfer is the error rate. Even the smallest disturbance in orientation will lead to a complete retransfer of data, creating bottlenecks in the quantum channel. Various error correcting codes are being researched but are still far from being implementable or even discussed in detail.

Limitations of quantum cryptography

1. Computers capable of transferring quantum information over a quantum channel are very large, complex and costly. Hence, only major IT firms, networking giants and a few well-supported educational institutes can pursue R&D in quantum cryptography. This leads to a monopoly and non-standard quantum information theories.
2. The error rate increases exponentially even if a fraction of sunlight interferes with the optic fibre cable. Even the most advanced shielding that exists today does not guarantee zero interference.
3. With increasing distances, qubits tend to become more error-prone. Amplifiers cannot be used in a quantum network, as it would make eavesdropper detection a difficult task. As a result, after a few hundred miles, the error rate becomes so high that reconstruction of qubits using entanglement is practically impossible.