SageMath: Deeper Insights into Cybersecurity

In the previous article in this SageMath series (published in the January 2025 issue of OSFY), we concluded our discussion of classical encryption techniques and moved on to the exploration of modern cryptography by looking at symmetric-key cryptography. In this ninth article in the series, we will continue the focus on symmetric-key cryptography.

In the last article, we wrote a SageMath program to implement a simple symmetric-key cryptographic algorithm called DES using a Python package called ‘PyCryptodome’. As promised, we will discuss the implementation of DES briefly in this article.

Most cryptography textbooks covering DES introduce a simplified version called the Simplified Data Encryption Standard (S-DES) to explain its working. S-DES follows the same fundamental principles as DES but operates on a smaller scale. It is a block cipher that encrypts 8-bit plaintext blocks using a 10-bit key, which is processed to generate two 8-bit subkeys for encryption and decryption. For a detailed analysis of S-DES, I recommend the classic textbook ‘Cryptography and Network Security: Principles and Practice’ by William Stallings. Let’s first explore the concept of block ciphers before examining how DES functions as one.

Block ciphers

A block cipher is an encryption method that processes data in fixed-size blocks, transforming plaintext into ciphertext using a secret key. A block cipher encrypts a block of N bits at a time (for example, DES uses 64-bit blocks). Each block is encrypted independently but may be linked to other blocks depending on the mode in which the block cipher operates.

In addition to DES, other examples of block ciphers include AES (Advanced Encryption Standard), which operates on a 128-bit block of data with key sizes of 128, 192, or 256 bits; Blowfish, which operates on a 64-bit block of data with a variable-length key ranging from 32 to 448 bits; and Twofish, which operates on a 128-bit block of data with key sizes up to 256 bits.

Now, let us return to our discussion of DES. It was developed by IBM and adopted as a standard by the US government in 1977. DES takes a 64-bit key but uses a 56-bit secret key after removing 8 parity bits from the original 64-bit key. Both the sender and the receiver must have the same key to encrypt and decrypt data. As mentioned earlier, DES is a block cipher. It encrypts data in 64-bit blocks, meaning it processes data in chunks of 64 bits at a time. Each 64-bit block undergoes 16 rounds of encryption, using a combination of substitutions and permutations (transpositions). These transformations mix the data in a complex way. After 16 rounds, the scrambled output obtained is the ciphertext (encrypted data). To decrypt, the same steps are applied in reverse, using the same key. Notice that DES utilises both the classical encryption techniques—substitution and transposition—which we have previously discussed in this series. However, these operations are executed in a much more advanced and intricate manner.

Almost all block ciphers employ a technique called a Feistel network, which is a cryptographic structure used to construct block ciphers. This network was developed by Horst Feistel, a German-American cryptographer, and was first used in the Feistel cipher, a predecessor to DES. Its simple yet elegant design consists of multiple rounds of processing. In each round, the block of data is divided into two halves. One half is encrypted using a substitution box (S-box), a permutation box (P-box), and a sub-key. An XOR operation is then performed between the encrypted half and the other half, followed by swapping the two halves. This process is repeated for multiple rounds, ultimately producing the encrypted block of data. The Feistel network’s unique structure allows for efficient encryption and decryption, making it an ideal framework for block ciphers like DES.

DES offers several modes of operation, each chosen based on specific security and performance requirements. The ECB (Electronic Codebook) mode encrypts each block independently. Though easy to implement, this mode is open to pattern attacks because identical plaintext blocks yield identical ciphertext. The CBC (Cipher Block Chaining) mode enhances security by performing an XOR operation on each plaintext block with the preceding ciphertext block before encryption, thereby obscuring patterns. The CFB (Cipher Feedback) mode and OFB (Output Feedback) mode effectively transform DES into a stream cipher (which we will discuss later), allowing encryption of smaller data units and providing resilience against bit-level manipulation. The CTR (Counter) mode leverages a counter value to generate keystream blocks, enabling parallel encryption and decryption for high-throughput applications. The choice of a particular mode depends on the trade-offs between security, efficiency, and error propagation.

Now that we have a clearer understanding of how DES operates, let us explore additional implementation options. In the previous article, we used the library ‘PyCryptodome’ to implement DES. However, there are multiple ways to implement cryptographic functions in SageMath. Recall that SageMath is essentially Python with added mathematical capabilities, which means any package or library accessible in Python can also be used in SageMath. Moreover, with Cython and Jython, it is possible to integrate C, C++, and Java code within Python. As a result, libraries written in these languages can also be leveraged within SageMath, providing greater flexibility in cryptographic implementations.

So, what other options do we have for implementing cryptographic functions? The aptly named library ‘Cryptography’ is designed to be both secure and user-friendly. It includes symmetric encryption algorithms like DES and AES, key derivation functions such as PBKDF2 and Argon2, as well as support for certificates and public-key cryptography. The ‘hashlib’ library, which is part of Python’s standard library, is used for hashing and supports algorithms like MD5, SHA-1, SHA-256, and SHA-512. Another option is ‘PyNaCl’, a Python binding to the ‘NaCl (libsodium)’ library, which focuses on secure and high-performance cryptographic operations. It provides authenticated encryption, digital signatures, and hashing. If terms like key derivation, certificates, and hashing are unfamiliar to you, don’t worry—we will explore these concepts in detail in the upcoming articles in this series.

SageMath can also access C libraries like ‘OpenSSL’, one of the most widely used cryptographic libraries, providing functions for SSL/TLS, encryption, decryption, and hashing. Another modern and user-friendly C library for cryptographic operations, ‘libsodium’, can also be utilised within SageMath. For C++-based cryptographic libraries, ‘Crypto++’, which offers a comprehensive suite of cryptographic algorithms, can be integrated into SageMath by creating Python bindings using ‘Cython’. Similarly, Java libraries such as ‘Bouncy Castle’ and the ‘Java Cryptography Architecture (JCA)’ can be accessed in SageMath through Jython, enabling the use of Java-based cryptographic functions.

Now, it is time to discuss some history. We have already seen that the US government adopted DES as its official standard in 1977. During the Cold War, the Soviet Union (now largely succeeded by Russia) developed its own cryptographic algorithm called GOST.

What about our country? Cryptography is closely tied to national security, and information regarding it is often difficult to find in the public domain. However, the limited available information suggests that India used the Indian Naval Cipher until the 1960s and later switched to DES in the 1970s. By the 1980s, we had started developing our own indigenous cryptographic systems.

The following story highlights the importance of developing our own cryptographic standards rather than blindly adopting those created by others. In the 1970s, when DES was designed, the concept of differential cryptanalysis (a type of attack on cryptographic algorithms) was not publicly known. However, the designers of DES—IBM and the NSA (National Security Agency of the US)—were aware of this potential vulnerability. To mitigate the risk, they modified the original S-box design to make it more resistant to differential cryptanalysis.

It wasn’t until the 1990s that Eli Biham and Adi Shamir independently discovered differential cryptanalysis and applied it to DES. They demonstrated that DES was indeed vulnerable to this attack, although exploiting it required an impractically large number of chosen plaintexts. When the NSA later announced that they had known about such attacks as early as the 1970s, it came as a surprise to many.

This raises an important question: Are we truly secure, or is there an agency secretly accessing our data by exploiting vulnerabilities that are not yet publicly known? Hopefully not. This concern has been widely discussed, even in fiction. For example, the novel ‘Digital Fortress’ by Dan Brown explores the world of encryption as its central theme.

The vulnerability of the S-box was not the primary threat to DES; rather, it was the relatively short key length of 64 bits, which became increasingly susceptible to attacks as faster computers were developed by the late 1970s. Triple DES (also known as 3DES) was introduced as an enhancement to the original Data Encryption Standard (DES) to address its vulnerability to brute-force attacks (where every possible key is systematically tried) due to its short 56-bit key (removing the 8 parity bits reduces the original 64-bit key to a 56-bit key). Triple DES applies the DES algorithm three times sequentially, using either two or three independent 56-bit keys, effectively increasing the key length to 112 or 168 bits. This significantly enhances security compared to DES, making brute-force attacks much more difficult.

Now, let us explore the implementation of Triple DES using the library ‘Cryptography’. In the previous article, we installed and began using SageMath on our computer instead of using the online tool CoCalc. We worked with the enhanced IPython-based interface to execute SageMath code in the terminal and learned how to run SageMath programs using the command sage. Similarly, in this article, we will execute the SageMath program locally on our machine rather than using CoCalc.

Now, consider the SageMath program shown below, which implements Triple DES using the library Cryptography. Notice that this is the 25^th program we are discussing in this series; thus, the program is aptly named ‘tripledes25.sage’ (line numbers are included for clarity).

Let us go through the code line by line to understand how it works. Line 1 imports the modules Cipher (used to create encryption and decryption objects), algorithms (provides different encryption algorithms like AES, TripleDES, etc), and modes (defines encryption modes like ECB, CBC, etc). Line 2 imports the module padding which provides functions for PKCS7 padding. This ensures that data size is a multiple of the block size. Line 3 imports the module default_backend which specifies the cryptographic backend required to create the Cipher object. Line 4 defines the encryption key as a byte string (indicated by b). Line 5 defines the plaintext message that will be encrypted. Line 6 prints the original plaintext before encryption. Line 7 creates a PKCS7 padder with a block size of 64 bits (8 bytes). Line 8 converts the plaintext into bytes using the function encode( ) and applies padding by using the functions padder.update( ) and padder.finalize( ), ensuring it matches the block size. Line 9 specifies TripleDES as the encryption algorithm, Electronic Codebook (ECB) as the mode, and also specifies the cryptographic backend. Line 10 creates an encryptor object from the cipher. Line 11 encrypts the padded plaintext by processing it in chunks. Line 12 prints the encrypted text as a hexadecimal string for readability. Line 13 creates a decryptor object from the cipher. Line 14 decrypts the ciphertext, but it still includes padding. Line 15 creates an unpadder object to remove PKCS7 padding. Line 16 removes the padding from the decrypted data. Finally, Line 17 decodes the decrypted bytes back into a human-readable string and prints the original plaintext.

Now, let us execute the SageMath program ‘tripledes25.sage’. The program can be executed by running the command sage tripledes25.sage in the terminal. Figure 1 shows the execution of the SageMath program ‘tripledes25.sage’. It can be observed in the figure that the ciphertext generated is the same as in the previous implementation of DES using ‘PyCryptodome’ when the plaintext and the secret key are identical. This is because we are still using an 8-byte key, effectively reducing the security of the algorithm to that of standard DES. Remember, TripleDES requires a 16-byte or 24-byte key to provide full cryptographic strength.

Now, let us familiarise ourselves with two fundamental principles in cryptography—confusion and diffusion—using the SageMath program ‘tripledes25.sage’. These concepts were introduced by Claude Shannon, a pioneer in communication and cryptography.

‘Confusion’ ensures that the relationship between the plaintext, ciphertext, and secret key is complex and unpredictable. This means that even a small change in the key significantly alters the ciphertext. To observe confusion in action, let us modify the key in ‘tripledes25.sage’ from “RAINBOWS” to “RAINBOWX” (a change in just a single character) and execute the program. The new ciphertext obtained is:

fd794da244887abc8bc7c9073247e61158a40f99cd966f6b. This ciphertext is completely different from the original: fffb961a5099b22543c7adf47c8c5ee061d52ff30cc349be. Despite changing just one character in the key, the output is unrecognisable, demonstrating strong confusion in the encryption process.

‘Diffusion’ ensures that every bit of plaintext spreads throughout the ciphertext, hiding statistical properties of the original message. A small change in the plaintext should affect multiple bits of the ciphertext—this is known as the avalanche effect. To observe diffusion, let us modify the plaintext from “HAPPINESSISABUTTERFLY” to “HAPPINESSISXBUTTERFLY”, changing just one letter. Upon execution, the new ciphertext is: fffb961a5099b22514035f3dcb702f4f61d52ff30cc349be. Comparing it with the original ciphertext, we see that 16 characters in the middle have changed:

This significant difference caused by a minor plaintext change highlights strong diffusion in the encryption process. If you ever design your own cryptographic algorithm—perhaps for an academic project—ensure that it incorporates both confusion and diffusion to enhance security.

The Advanced Encryption Standard (AES)

Though Triple DES replaced DES, it was slower due to its triple encryption process and remained vulnerable to certain cryptographic attacks, such as meet-in-the-middle attack. Because of these limitations, Triple DES was eventually replaced by the Advanced Encryption Standard (AES), which offers stronger security, better performance, and greater efficiency in both software and hardware implementations. Originally known as Rijndael, AES was developed by cryptographers Joan Daemen and Vincent Rijmen and was adopted by the US-based National Institute of Standards and Technology (NIST) in 2001. The National Centre for Communication Security (NCCS) in India also recommends AES.

Now, consider the SageMath program named ‘aes26.sage’ shown below, which implements AES using the package ‘PyCryptodome’.

A detailed discussion of the program is omitted due to space constraints. Also, a discussion of the workings of AES is beyond the scope of this series. Therefore, let us briefly explain the SageMath program ‘aes26.sage’. This program implements AES in Cipher Block Chaining (CBC) mode. The function pad( ) ensures that the plaintext length is a multiple of 16 bytes by adding padding characters, while the function unpad( ) removes them after decryption. The function encrypt_aes( ) first pads the plaintext, then initialises an AES cipher object with a randomly generated 16-byte key, and encrypts the data using CBC mode. The initialisation vector (IV) and ciphertext are then base64-encoded for safe storage or transmission. The function decrypt_aes( ) reverses this process by extracting the IV, decrypting the ciphertext, and removing the padding to recover the original message. Finally, the program generates a random AES key, encrypts the string “Open Source For you”, and then decrypts it, demonstrating that the encryption and decryption processes work correctly. Note that because a random key is used each time, the generated ciphertext will be different with each execution of the program. Upon execution of the program ‘aes26.sage’, the output shown in Figure 2 will be displayed on the terminal.

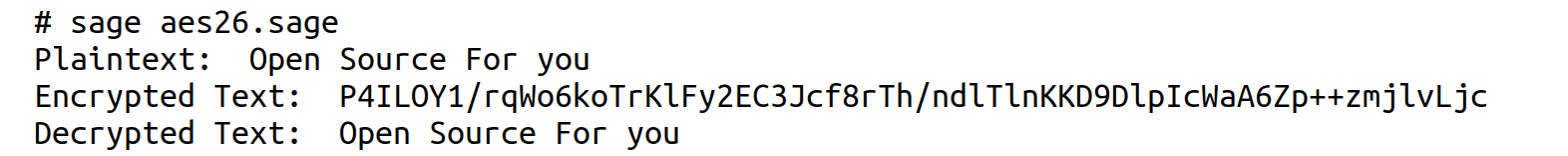
Stream ciphers

The story of symmetric-key cryptography does not end with block ciphers alone; stream ciphers must also be considered. A stream cipher is a type of symmetric encryption algorithm that encrypts data one bit or byte at a time, rather than processing it in fixed-size blocks, as in block ciphers like DES, Triple DES, and AES. This makes stream ciphers fast, efficient, and ideal for applications requiring real-time encryption. However, stream ciphers have a vulnerability: if the same keystream is used to encrypt multiple messages, an attacker can recover the plaintext. ChaCha20, Salsa20, XSalsa20, Grain, and RC4 are examples of stream ciphers.

Now, consider the SageMath program named ‘stream27.sage’ shown below which implements XSalsa20 stream cipher. XSalsa20 is a stream cipher that extends the Salsa20 stream cipher by using a 192-bit nonce instead of a 64-bit nonce, making it more secure against nonce reuse attacks. A nonce (number used once) is a unique, randomly chosen or sequentially incremented value used to ensure that encryption is non-deterministic. This prevents attackers from detecting patterns in encrypted messages. XSalsa20 and Salsa20 were designed by Daniel J. Bernstein and are part of the ‘NaCl’ (Networking and Cryptography Library). The program ‘stream27.sage’ uses the library ‘PyNaCl’ for secret-key encryption and ‘PyCryptodome’ for padding and unpadding plaintext (line numbers are included for clarity).

Now, let us go through the code line by line to understand how it works. Line 1 imports nacl.secret, which provides secret-key encryption using the XSalsa20 encryption algorithm with Poly1305 authentication. Line 2 imports nacl.utils, which contains utility functions like random key generation. Line 3 imports the functions pad( ) and unpad( ) from the module Crypto.Util.Padding offered by ‘PyCryptodome’. In Line 4, the encryption key is generated from the string “RAINBOWS”, which is repeated 4 times to form b“RAINBOWSRAINBOWSRAINBOWSRAINBOWS”. The index [:32] ensures that only the first 32 bytes are used (as required by nacl.secret.SecretBox, which expects a 32-byte key). Line 5 defines the plaintext message “HAPPINESSISABUTTERFLY”, which will be encrypted. Line 6 prints the plaintext before encryption. Line 7 initialises an instance named box of SecretBox using the key generated. In Line 8, the function encode( ) converts the plaintext string into bytes and the function pad( ) applies PKCS7 padding to make the plaintext’s length a multiple of 8 bytes. Line 9 encrypts the padded plaintext using XSalsa20 encryption and authenticates with Poly1305 authentication. Line 10 extracts and prints the ciphertext in hexadecimal format. Line 11 decrypts ciphertext using the instance box of SecretBox. Line 12 removes the PKCS7 padding using the function unpad( ) and converts the bytes back to a string. Finally, Line 13 prints the decrypted message. Upon execution of the SageMath program ‘stream27.sage’, the output shown in Figure 3 will be displayed on the terminal.

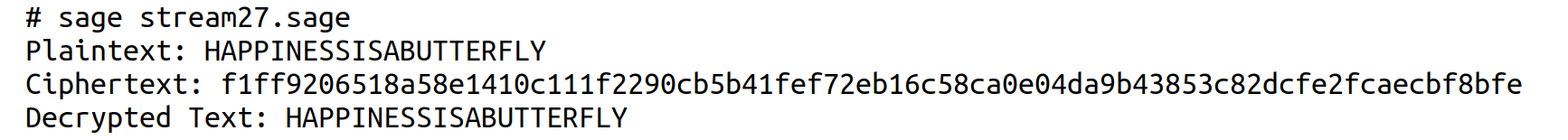
As we wrap up this article, I can say with some satisfaction that we have covered as much theory and code as possible within the few pages available in a popular magazine like OSFY to discuss symmetric-key encryption. However, note that we have only seen the tip of the iceberg. To gain a better understanding of the implementation details of DES, Triple DES, AES, etc, I once again recommend the classic textbook ‘Cryptography and Network Security: Principles and Practice’ by William Stallings.

In the next article in this series, we will delve into public-key cryptography—a concept that is surprising, counter-intuitive, and fundamentally at odds with the principles of encryption that have evolved over two millennia. Stay tuned!