In the previous articles in this SageMath series, we delved into graph theory and explored its applications using SageMath. In this seventh article in the series, it is time to shift our focus to another crucial subfield of computer science: cybersecurity and cryptography.

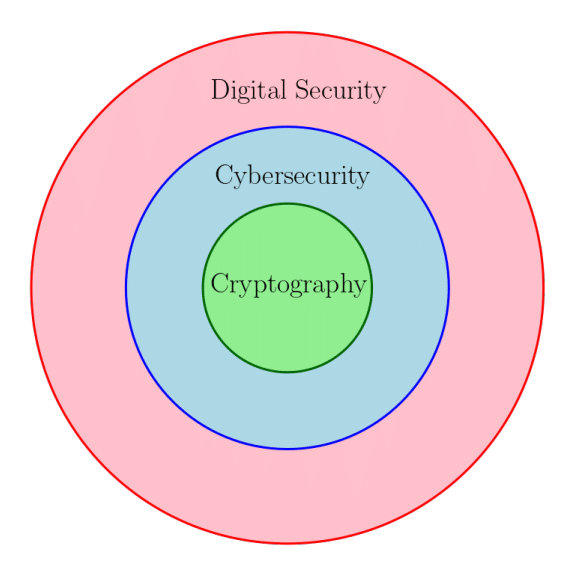
Before diving deeper into the technical discussion, it is important to clarify a key point. While cybersecurity is a popular buzzword in the IT industry, we need to compare three widely used terms: digital security, cybersecurity, and cryptography. How are they related? There are varying viewpoints on the relationship between these fields. Figure 1 represents this relationship as a Venn diagram, illustrating how these concepts are related.

Digital security is the broadest of the three and encompasses all measures aimed at protecting digital assets and information. This includes strategies, technologies, and practices designed to safeguard digital data, devices, and systems from unauthorised access, damage, or loss, whether online or offline.

Cybersecurity is a more focused subset of digital security, dedicated specifically to defending digital systems and data from threats that arise in cyberspace. It involves protecting computer systems, networks, and online resources from cyberattacks, such as hacking, malware, phishing, and other forms of cybercrime.

Cryptography, in turn, is a specialised branch of cybersecurity. It involves securing information through mathematical techniques and algorithms, ensuring data confidentiality, integrity, and authenticity. Cryptography works by encoding data to prevent unauthorised access or tampering. In this series, we will focus primarily on cryptographic methods that can be implemented using SageMath.

Now, let us explore the important fields of study in cryptography. These include classical encryption schemes, symmetric key cryptography (also known as private key cryptography or secret key cryptography), asymmetric key cryptography (also known as public key cryptography), digital signatures, key exchange protocols, hash functions, zero-knowledge proofs, post-quantum cryptography, steganography, quantum cryptography, etc. We will cover many of these topics within the scope of this series in a straightforward manner to ensure that everyone can follow along and engage with the discussion.

Before we proceed, it is important to understand two key terms: encryption and decryption. Encryption is the process of transforming readable data, known as plaintext, into an unreadable format called ciphertext. This ensures that the data remains confidential and protected from unauthorised access. It also safeguards the data’s integrity and authenticity, ensuring it has not been altered or tampered with. Decryption is the reverse process, where the ciphertext (unreadable data) is converted back into plaintext (readable data). This allows the intended recipient to access the original message securely.

In cryptographic discussions, fictional characters are often used to illustrate various scenarios and algorithms. The classic names include Alice (A): the sender or initiator of secure communication, and Bob (B): the recipient or responder. Eve (E) represents an eavesdropper attempting to intercept or compromise the communication, while Mallory (M) stands for a malicious attacker, often illustrating active attacks. For example, when Alice wants to send a secure message to Bob, Eve may try to intercept it, or Mallory might attempt to alter it. Additional characters include Charlie (C), sometimes used as an intermediary or third party, and Dave (D), who may represent an additional participant. Trent (T) often represents a trusted third party or authority, while Victor (V) is used in scenarios involving zero-knowledge proofs and acts as the verifier. Although I considered using Indian names to add a local flavour, I refrained because all the classic cryptography textbooks use names like Alice and Bob. We will follow this convention throughout our discussions to maintain consistency with the standard references.

Cryptography involves a lot of mathematics, but my aim is to make this discussion as accessible as possible with minimal math. So, before we dive into the mathematical aspects of cybersecurity, let me start with a story. Alice wants to send a secret message to Bob. She has a box, along with a lock and key. Alice puts the secret message in the box, locks it with her key, and sends the box to Bob through Trent. However, Bob can’t open the box because he doesn’t have the key. Now, Alice also needs to send the key to Bob through Trent. But here is the problem: Can Alice really trust Trent? What if Trent opens the box and reads the secret message? Sending both the locked box and the key with the same person isn’t always safe.

Realising this, Alice tries a different strategy. She locks the box with her key and sends it to Bob. Bob, unable to open it, adds his own lock to the box and sends it back to Alice. Alice unlocks her lock and sends the box back to Bob, who can now unlock it with his own key and open the box. In this way, the keys are never transported, but the box has to be exchanged multiple times between Alice and Bob. This simple story highlights many of the key challenges in cryptography: sending secret messages, managing keys, and trusting third parties. In this series, we will explore how cryptographic algorithms and SageMath methods can solve these challenges efficiently.

Classical encryption schemes

Let us begin our discussion with classical encryption schemes. These are called ‘classical’ because they have been around for a very long time. For example, the Caesar cipher, named after Julius Caesar (ruler of Rome from 49 BC to 44 BC), has been in use for over two millennia. It is important to note that Julius Caesar didn’t invent the Caesar cipher; he simply popularised it by using it in his personal correspondence.

Caesar cipher

The Caesar cipher is one of the simplest ciphers that has ever existed. Most of us are familiar with it and may have even used it for fun during our school days. To demonstrate how it works, let us use the string ‘I READ OSFY’ as our plaintext. In a Caesar cipher, each letter in the plaintext is shifted by a certain number of positions down the alphabet. In this case, we will shift every letter three positions forward (Julius Caesar himself used a shift of three positions). For example, A becomes D, B becomes E, C becomes F, and so on. Let us go through the encryption step by step. The letter ‘I’ shifts to ‘L’ (I→J→K→L), ‘R’ shifts to ‘U’ (R→S→T→U), ‘E’ shifts to ‘H’ (E→F→G→H), and so on. But what happens with the letter ‘Y’? Since it is at the end of the alphabet, when we shift it forward three positions, we wrap around to the beginning of the alphabet. This is like how a clock works: after 12 o’clock, the next hour is 1, not 13. So, ‘Y’ shifts to ‘B’ (Y→Z→A→B). This wrap-around effect is an example of modular arithmetic, a concept often used in cryptography. It means that after reaching the maximum letter (Z), we start again from the beginning (A). Just like on a clock, after 12 comes 1, and after ‘Z’, we return to ‘A’. Thus, after applying the Caesar cipher with a shift of three, the original message ‘I READ OSFY’ becomes ‘L UHDG RVIB’.

To decrypt the ciphertext, we reverse the process by shifting each letter three positions backward in the alphabet. Let us see how the ciphertext ‘L UHDG RVIB’ is decrypted. The letter ‘L’ shifts back to ‘I’ (L→K→J→I), ‘U’ shifts back to ‘R’ (U→T→S→R), ‘H’ shifts back to ‘E’ (H→G→F→E), and so on. Finally, the decrypted message obtained is ‘I READ OSFY’, which is the same as the original plaintext.

Let us now implement the Caesar cipher with a shift of three using SageMath. The program ‘caesar20.sagews’, shown below, implements Caesar cipher (line numbers are included for clarity).

1. def caesar_cipher(text, shift):

2. result = “”

3. for char in text:

4. if char.isalpha( ):

5. new_pos = (ord(char)-ord(‘A’)+shift)%26

6. new_char = chr(new_pos + ord(‘A’))

7. result += new_char

8. else:

9. result += char

10. return result

Now, let us go through the code line by line to understand how it works. Line 1 defines a function named caesar_cipher( ) that takes two arguments: text (the string to be encrypted or decrypted) and shift (the number of positions each letter will be shifted in the alphabet). Line 2 initialises an empty string called result, where the encrypted text will be stored as the function processes each character from the input text. Line 3 starts a loop that iterates over each character in the input text. Line 4 checks if the current character is an alphabetic letter (A-Z or a-z). If the character is a letter, it will be shifted; if not (for example, a space or punctuation), it will be left unchanged. In Line 5, ord(char) gets the Unicode (also ASCII) value of the current character. For example, ord(‘A’) returns 65. The value given by ord(‘A’) is subtracted to convert the character’s ASCII value into a range that starts from 0 for ‘A’ (for example, ‘A’ is treated as 0, ‘B’ as 1, etc). Then, the value of the shift is added to shift the position of the character in the alphabet. The modulus operation (%) by 26 ensures that the result wraps around if it goes beyond ‘Z’. Line 6 converts the shifted position back to the corresponding ASCII value and then converts this ASCII value back to a character and stores it in new_char. Line 7 adds the newly encrypted character in new_char to the string result. The else in Line 8 is executed only if the current character is not alphabetic. Line 9 adds this character unchanged to the string result. Once all characters have been processed, in Line 10, the function returns the string result, which contains the fully encrypted text or decrypted text.

Now, we need to test this Caesar cipher function using plaintext. The following lines of code are added to the end of the function caesar_cipher( ) to perform this testing (line numbers are included for clarity).

11. plaintext = “I READ OSFY”

12. shift = 3

13. encrypted_text = caesar_cipher(plaintext, shift)

14. print(“Encrypted text:”, encrypted_text)

15. decrypted_text = caesar_cipher(encrypted_text, -shift)

16. print(“Decrypted text:”, decrypted_text)

Let us try to understand how the testing works. Line 11 assigns the string ‘I READ OSFY’ to the variable plaintext. This is the text that we want to encrypt using the Caesar cipher. Line 12 sets the variable shift to 3, meaning each letter in the plaintext will be shifted by three positions in the alphabet during encryption. For example, ‘A’ becomes ‘D’, ‘B’ becomes ‘E’, and so on. Line 13 calls the function caesar_cipher( ) with two arguments: plaintext and shift (3). The function encrypts the plaintext by shifting each alphabetic character by three positions. The result of this encryption is stored in the variable encrypted_text. Line 14 prints the encrypted version of the plaintext. Line 15 decrypts the encrypted_text by calling the function caesar_cipher( ) again, but this time with the shift value as -3. The negative shift reverses the encryption, restoring the text to its original form. The decrypted text is stored in the variable decrypted_text. Line 16 prints the decrypted version of the encrypted text, which should match the original plaintext.

Now, let us execute the program ‘caesar20.sagews’. As before, we will use the online tool called CoCalc to run the program. Upon execution, the following output will be displayed on the screen.

Encrypted text: L UHDG RVIB

Decrypted text: I READ OSFY

Notice that the encrypted text is neither meaningful nor similar to the plaintext. Now, let us modify Line 12 of the code to shift = 4 and observe the output. Upon running the modified program, the encrypted text displayed is ‘M VIEH SWJC’, which is different from the encrypted text when the shift was 3. However, as before, the decrypted text remains ‘I READ OSFY’, matching the original plaintext. Next, we will try a shift of 26 by updating Line 12 to shift = 26. When the program is executed, the encrypted text displayed is ‘I READ OSFY’, identical to the plaintext. This occurs because a shift of 26 cycles of the alphabet returns it back to its original positions; hence, each letter remains unchanged. Therefore, only shifts between 1 and 25 are meaningful in Caesar cipher, as a shift of 0 also leaves the text unchanged.

The Caesar cipher is a type of monoalphabetic substitution cipher, where each letter in the plaintext is consistently replaced by a letter from a fixed substitution alphabet. In monoalphabetic substitution ciphers, the same letter is always substituted by the same corresponding letter throughout the entire message. The security of the Caesar cipher relies on the attacker not knowing the shift value. However, as we have already observed, there are only 25 possible shifts, making it easy for an attacker to try all of them and quickly discover the plaintext. This method of attack is known as a brute-force attack. Because of this vulnerability, the Caesar cipher and similar monoalphabetic substitution ciphers are considered ineffective for secure communication. This limitation has led to the development of more advanced and harder-to-crack encryption methods, such as polyalphabetic substitution ciphers.

Vigenère cipher

Polyalphabetic substitution ciphers use multiple substitution alphabets to encrypt a message, making them more secure than monoalphabetic substitution ciphers. In this method, the same letter can be replaced by different letters depending on its position in the text, which reduces patterns and makes frequency analysis attacks more difficult. The Vigenère cipher (invented by Giovan Battista Bellaso in 1553 but misnamed after Blaise de Vigenère) is a well-known polyalphabetic cipher that uses a repeating key (a group of random characters) to shift letters by different amounts. Each letter in the key corresponds to a different Caesar cipher, and the shifts are applied in a cycle. This way, the same plaintext letter can be substituted by different ciphertext letters based on its position in the sequence, enhancing security.

Let us try to understand the working of the Vigenère cipher using the plaintext ‘BCDEFBCDE’ and the key ‘BCD’. We will first define how letter values are assigned. In the Vigenère cipher, each letter corresponds to a numerical value as follows: A = 0, B = 1, C = 2, D = 3, E = 4, and so on up to Z = 25. Now, we will walk through the encryption using the key ‘BCD’. The plaintext values (using A = 0, B = 1, etc) are B = 1, C = 2, D = 3, E = 4, F = 5, B = 1, C = 2, D = 3, and E = 4. Key values (repeated to match the length of the plaintext) are B = 1, C = 2, D = 3, B = 1, C = 2, D = 3, B = 1, C = 2, and D = 3. The encryption happens as follows. Ciphertext values are obtained as (plaintext + key) mod 26. You can understand the working of the modulus operation by recalling the example of a clock. The corresponding positions of the letters in the plaintext, key, and ciphertext are shown below.

B C D E F B C D E
B C D B C D B C D
-----------------
C E G F H E D F H

Now, let us go through the encryption process in detail. We get: (B+B)→(1+1)=2→C, (C+C)→(2+2)=4→E, (D+D)→(3+3)=6→G, (E+B)→(4+1)=5→F, (F+C)→(5+2)=7→H, (B+D)→(1+3)=4→E, (C+B)→(2+1)=3→D, (D+C)→(3+2)=5→F, and (E+D)→(4+3)=7→H. Thus, the final ciphertext is CEGFHEDFH. Keep in mind that the first ‘B’ in the plaintext became a ‘C’ and the second ‘B’ became an ‘E’. Similarly, the first ‘E’ in the cipher text is a substitution for the letter ‘C’ in the plaintext and the second ‘E’ is a substitution for the letter ‘B’ in the plaintext. This is different from the Caesar cipher. In this way, polyalphabetic substitution ciphers like Vigenère cipher are far stronger than a Caesar cipher.

Let us now implement the Vigenère cipher using SageMath. The program ‘vigenere21.sagews’, as shown below, implements a Vigenère cipher function that can both encrypt and decrypt text based on the given key and mode (line numbers are included for clarity). For simplicity, the program assumes that both the plaintext and the key consist solely of uppercase letters from the English alphabet, with no spaces or special characters allowed.

1. def vigenere_cipher(data, key, mode):

2. alphabet = ‘ABCDEFGHIJKLMNOPQRSTUVWXYZ’

3. text = [ ]

4. key_length = len(key)

5. for i, char in enumerate(data):

6. shift = alphabet.index(key[i % key_length]) * mode

7. new_char = alphabet[(alphabet.index(char) + shift) % 26]

8. text.append(new_char)

9. return ‘’.join(text)

Now, let us go through the code line by line to understand how it works. Line 1 defines a function named vigenere_cipher( ), which takes three arguments: data (the text to be encrypted or decrypted), key (the string used for encryption or decryption), and mode (an integer that determines whether the function will encrypt or decrypt). In Line 2, a string containing all the uppercase letters of the English alphabet is assigned to the variable alphabet. This will be used to look up the positions of letters. Line 3 initialises an empty list named text, which will store the processed characters (either encrypted or decrypted) as the function iterates over the input data. Line 4 calculates the length of the key string and stores it in the variable key_length. This will help determine how to cycle through the key during the encryption or decryption process. Line 5 starts a loop that iterates over each character in the data string. The enumerate( ) function is used to get both the index and the character in each iteration. Line 6 calculates the shift amount for the current character based on the corresponding character in the key. The code alphabet.index(key[i % key_length]) gives the position of the key’s character in the alphabet. The modulus operation (i % key_length) ensures that the key repeats if it is shorter than the data. Finally, mode is multiplied by the shift value. If mode is 1, the character will be shifted forward (encryption). If mode is -1, the character will be shifted backward (decryption). Line 7 calculates the new character after shifting. The code alphabet.index(char) gives the position of the current character in the alphabet. The shift value is added to this index for encryption or subtracted for decryption. The modulus operation (% 26) ensures that the index wraps around within the alphabet if it exceeds 25. Then, the index of the string alphabet retrieves the character corresponding to the new shifted position. Line 8 appends the newly calculated character in new_char to the list text, building the result step by step. Finally, after all characters have been processed, Line 9 joins the list text into a single string and returns the result, either the fully encrypted or decrypted text.

Now, we need to test this Vigenère cipher function using a plaintext and a key. The following lines of code are added to the end of the function vigenere_cipher( ) to perform this testing (line numbers are included for clarity).

10. plaintext = “CRYPTOGRAPHY”

11. key = “BCDE”

12. ciphertext = vigenere_cipher(plaintext, key, 1)

13. print(“Encrypted:”, ciphertext)

14. decrypted_text = vigenere_cipher(ciphertext, key, -1)

15. print(“Decrypted:”, decrypted_text)

This code for testing the function vigenere_cipher( ) is very similar to the code used to test the function caesar_cipher( ). The main difference is that, instead of using a fixed shift, the Vigenère cipher uses a key (Line 14). As mentioned earlier, a mode value of 1 is used for encryption, and a mode value of -1 is used for decryption.

Now, let us execute the program ‘vigenere21.sagews’. Upon execution, the following output will be displayed on the screen.

Encrypted: DTBTUQJVBRKC

Decrypted: CRYPTOGRAPHY

The output once again confirms that the plaintext and ciphertext are in no way related, and it also demonstrates that encryption with the Vigenère cipher is reversible. Now, try the key ‘MXQZVAIXOZHQ’ by changing the code in Line 17 to key = “MXQZVAIXOZHQ”. Upon executing the modified code, the encrypted text obtained is ‘OOOOOOOOOOOO’. Funny, isn’t it? From the output, it can also be verified that the correct plaintext is obtained upon decryption.

The security of the Vigenère cipher relies heavily on the secrecy of the key. If the key is compromised, the cipher can be easily broken. For over three centuries, the Vigenère cipher was believed to be unbreakable. The French even referred to it as ‘le chiffrage indéchiffrable’ (the indecipherable cipher). However, in 1863, Friedrich Kasiski, a military officer from Prussia (a German-speaking nation that later became a key part of Germany), published a method for breaking the Vigenère cipher by analysing repeated sequences in the ciphertext. This technique, known as the ‘Kasiski examination’, allowed cryptanalysts (people who study and break codes and ciphers to uncover hidden information) to deduce the key length by exploiting patterns in the encrypted message, marking a major breakthrough in cryptography.

Just eight years later, in 1871, Prussia defeated France in the Franco-Prussian War, leading to the formation of the German Empire. While it’s uncertain whether the breaking of French military Vigenère cipher codes directly contributed to their defeat, Kasiski’s method undeniably weakened the perception of the cipher’s invincibility. Could the cipher’s compromise have played a part in France’s downfall? Perhaps.

This article provided a gentle introduction to the terminology used in cybersecurity and related areas. We also explored the implementation details of two important classical encryption schemes, albeit in a simplified manner, and implemented them using SageMath. Notably, the code we discussed is predominantly Python, once again highlighting SageMath’s ability to extend Python’s capabilities.

In the next article in this SageMath series, we will continue our exploration of classical encryption schemes by examining transposition ciphers, which scramble the positions of characters rather than altering the characters themselves. We will also begin our discussion on symmetric key cryptography, also known as private key cryptography or secret key cryptography, along with its implementation in SageMath.