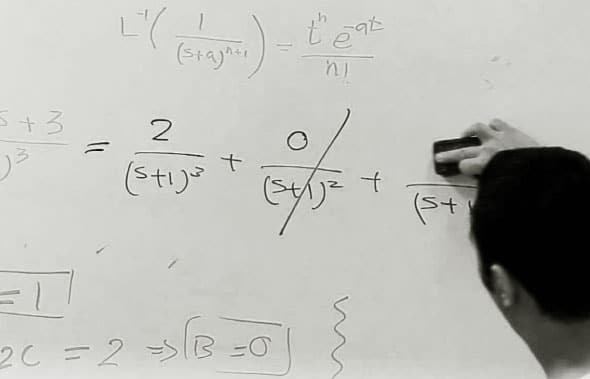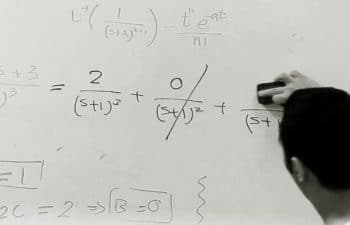
In higher mathematics, transforms play an important role. A transform is mathematical logic to transform or convert a mathematical expression into another mathematical expression, typically from one domain to another. Laplace and Fourier are two very common examples, transforming from the time domain to the frequency domain. In general, such transforms have their corresponding inverse transforms. And this combination of direct and inverse transforms is very powerful in solving many real life engineering problems. The focus of this article is Laplace and its inverse transform, along with some problem-solving insights.
The Laplace transform
Mathematically, the Laplace transform F(s) of a function f(t) is defined as follows:
F(s) =∫∞0ƒ(t)*exp(–s*t)dt
where t represents time and s represents complex angular frequency.
To demonstrate it, lets take a simple example of f(t) = 1. Substituting and integrating, we get F(s) = 1/s. Maxima has the function laplace() to do the same. In fact, with that, we can choose to let our variables t and s be anything else as well. But, as per our mathematical notations, preserving them as t and s would be the most appropriate. Lets start with some basic Laplace transforms. (Note that string() has been used to just flatten the expression.)
$ maxima -q(%i1) string(laplace(1, t, s));(%o1) 1/s(%i2) string(laplace(t, t, s));(%o2) 1/s^2(%i3) string(laplace(t^2, t, s));(%o3) 2/s^3(%i4) string(laplace(t+1, t, s));(%o4) 1/s+1/s^2(%i5) string(laplace(t^n, t, s));Is n + 1 positive, negative, or zero?p; /* Our input */(%o5) gamma(n+1)*s^(-n-1)(%i6) string(laplace(t^n, t, s));Is n + 1 positive, negative, or zero?n; /* Our input */(%o6) gamma_incomplete(n+1,0)*s^(-n-1)(%i7) string(laplace(t^n, t, s));Is n + 1 positive, negative, or zero?z; /* Our input, making it non-solvable */(%o7) laplace(t^n,t,s)(%i8) string(laplace(1/t, t, s)); /* Non-solvable */(%o8) laplace(1/t,t,s)(%i9) string(laplace(1/t^2, t, s)); /* Non-solvable */(%o9) laplace(1/t^2,t,s)(%i10) quit(); |
In the above examples, the expression is preserved as is, in case of non-solvability.
laplace() is designed to understand various symbolic functions, such as sin(), cos(), sinh(), cosh(), log(), exp(), delta(), erf(). delta() is the Dirac delta function, and erf() is the error functionothers being the usual mathematical functions.
$ maxima -q(%i1) string(laplace(sin(t), t, s));(%o1) 1/(s^2+1)(%i2) string(laplace(sin(w*t), t, s));(%o2) w/(w^2+s^2)(%i3) string(laplace(cos(t), t, s));(%o3) s/(s^2+1)(%i4) string(laplace(cos(w*t), t, s));(%o4) s/(w^2+s^2)(%i5) string(laplace(sinh(t), t, s));(%o5) 1/(s^2-1)(%i6) string(laplace(sinh(w*t), t, s));(%o6) -w/(w^2-s^2)(%i7) string(laplace(cosh(t), t, s));(%o7) s/(s^2-1)(%i8) string(laplace(cosh(w*t), t, s));(%o8) -s/(w^2-s^2)(%i9) string(laplace(log(t), t, s));(%o9) (-log(s)-%gamma)/s(%i10) string(laplace(exp(t), t, s));(%o10) 1/(s-1)(%i11) string(laplace(delta(t), t, s));(%o11) 1(%i12) string(laplace(erf(t), t, s));(%o12) %e^(s^2/4)*(1-erf(s/2))/s(%i13) quit(); |
Interpreting the transform
A Laplace transform is typically a fractional expression consisting of a numerator and a denominator. Solving the denominator, by equating it to zero, gives the various complex frequencies associated with the original function. These are called the poles of the function. For example, the Laplace transform of sin(w * t) is w/(s^2 + w^2), where the denominator is s^2 + w^2. Equating that to zero and solving it, gives the complex frequency s = +iw, -iw; thus, indicating that the frequency of the original expression sin(w * t) is w, which indeed it is. Here are a few demonstrations of the same:
$ maxima -q(%i1) string(laplace(sin(w*t), t, s));(%o1) w/(w^2+s^2)(%i2) string(denom(laplace(sin(w*t), t, s))); /* The Denominator */(%o2) w^2+s^2(%i3) string(solve(denom(laplace(sin(w*t), t, s)), s)); /* The Poles */(%o3) [s = -%i*w,s = %i*w](%i4) string(solve(denom(laplace(sinh(w*t), t, s)), s));(%o4) [s = -w,s = w](%i5) string(solve(denom(laplace(cos(w*t), t, s)), s));(%o5) [s = -%i*w,s = %i*w](%i6) string(solve(denom(laplace(cosh(w*t), t, s)), s));(%o6) [s = -w,s = w](%i7) string(solve(denom(laplace(exp(w*t), t, s)), s));(%o7) [s = w](%i8) string(solve(denom(laplace(log(w*t), t, s)), s));(%o8) [s = 0](%i9) string(solve(denom(laplace(delta(w*t), t, s)), s));(%o9) [](%i10) string(solve(denom(laplace(erf(w*t), t, s)), s));(%o10) [s = 0](%i11) quit(); |
Involved Laplace transforms
laplace() also understands derivative() / diff(), integrate(), sum(), and ilt() – the inverse Laplace transform. Here are some interesting transforms showing the same:
$ maxima -q(%i1) laplace(f(t), t, s);(%o1) laplace(f(t), t, s)(%i2) string(laplace(derivative(f(t), t), t, s));(%o2) s*laplace(f(t),t,s)-f(0)(%i3) string(laplace(integrate(f(x), x, 0, t), t, s));(%o3) laplace(f(t),t,s)/s(%i4) string(laplace(derivative(sin(t), t), t, s));(%o4) s/(s^2+1)(%i5) string(laplace(integrate(sin(t), t), t, s));(%o5) -s/(s^2+1)(%i6) string(sum(t^i, i, 0, 5));(%o6) t^5+t^4+t^3+t^2+t+1(%i7) string(laplace(sum(t^i, i, 0, 5), t, s));(%o7) 1/s+1/s^2+2/s^3+6/s^4+24/s^5+120/s^6(%i8) string(laplace(ilt(1/s, s, t), t, s));(%o8) 1/s(%i9) quit(); |
Note the usage of ilt() – inverse Laplace transform in the %i8 of the above example. Calling laplace() and ilt() one after the other cancels their effectthat is what is meant by inverse. Lets look into some common inverse Laplace transforms.
Inverse Laplace transforms
$ maxima -q(%i1) string(ilt(1/s, s, t));(%o1) 1(%i2) string(ilt(1/s^2, s, t));(%o2) t(%i3) string(ilt(1/s^3, s, t));(%o3) t^2/2(%i4) string(ilt(1/s^4, s, t));(%o4) t^3/6(%i5) string(ilt(1/s^5, s, t));(%o5) t^4/24(%i6) string(ilt(1/s^10, s, t));(%o6) t^9/362880(%i7) string(ilt(1/s^100, s, t));(%o7) t^99/933262154439441526816992388562667004907159682643816214685929638952175999932299156089414639761565182862536979208272237582511852109168640000000000000000000000(%i8) string(ilt(1/(s-a), s, t));(%o8) %e^(a*t)(%i9) string(ilt(1/(s^2-a^2), s, t));(%o9) %e^(a*t)/(2*a)-%e^-(a*t)/(2*a)(%i10) string(ilt(s/(s^2-a^2), s, t));(%o10) %e^(a*t)/2+%e^-(a*t)/2(%i11) string(ilt(1/(s^2+a^2), s, t));Is a zero or nonzero?n; /* Our input */(%o11) sin(a*t)/a(%i12) string(ilt(s/(s^2+a^2), s, t));Is a zero or nonzero?n; /* Our input */(%o12) cos(a*t)(%i13) assume(a < 0) or assume(a > 0)$(%i14) string(ilt(1/(s^2+a^2), s, t));(%o14) sin(a*t)/a(%i15) string(ilt(s/(s^2+a^2), s, t));(%o15) cos(a*t)(%i16) string(ilt((s^2+s+1)/(s^3+s^2+s+1), s, t));(%o16) sin(t)/2+cos(t)/2+%e^-t/2(%i17) string(laplace(sin(t)/2+cos(t)/2+%e^-t/2, t, s));(%o17) s/(2*(s^2+1))+1/(2*(s^2+1))+1/(2*(s+1))(%i18) string(rat(laplace(sin(t)/2+cos(t)/2+%e^-t/2, t, s)));(%o18) (s^2+s+1)/(s^3+s^2+s+1)(%i19) quit(); |
Observe that if we take the Laplace transform of the above %o outputs, they would give back the expressions, which are input to ilt() of the corresponding %is. %i18 specifically shows one such example. It does laplace() of the output at %o16, giving back the expression, which was input to ilt() of %i16.
Solving differential and integral equations
Now, with these insights, we can easily solve many interesting and otherwise complex problems. One of them is solving differential equations. Lets explore a simple example of solving f(t) + f(t) = e^t, where f(0) = 0. First, lets take the Laplace transform of the equation. Then substitute the value for f(0), and simplify to obtain the Laplace of f(t), i.e., F(s). Finally, compute the inverse Laplace transform of F(s) to get the solution for f(t).
$ maxima -q(%i1) string(laplace(diff(f(t), t) + f(t) = exp(t), t, s));(%o1) s*laplace(f(t),t,s)+laplace(f(t),t,s)-f(0) = 1/(s-1) |
Substituting f(0) as 0, and then simplifying, we get laplace(f(t),t,s) = 1/((s-1)*(s+1)), for which we do an inverse Laplace transform:
(%i2) string(ilt(1/((s-1)*(s+1)), s, t));(%o2) %e^t/2-%e^-t/2(%i3) quit(); |
That gives us f(t) = (e^t e^-t) / 2, i.e., sinh(t), which definitely satisfies the given differential equation.
Similarly, we can solve equations with integrals. And not just integrals, but also equations with both differentials and integrals. Such equations come up very often when solving problems linked to electrical circuits with resistors, capacitors and inductors. Lets again look at a simple example that demonstrates the fact. Lets assume we have a 1 ohm resistor, a 1 farad capacitor, and a 1 henry inductor in series being powered by a sinusoidal voltage source of frequency w. What would be the current in the circuit, assuming it to be zero at t = 0? It would yield the following equation: R * i(t) + 1/C * ? i(t) dt + L * di(t)/dt = sin(w*t), where R = 1, C = 1, L =1.
So, the equation can be simplified to i(t) + ? i(t) dt + di(t)/dt = sin(w*t). Now, following the procedure as described above, lets carry out the following steps:
$ maxima -q(%i1) string(laplace(i(t) + integrate(i(x), x, 0, t) + diff(i(t), t) = sin(w*t), t, s));(%o1) s*laplace(i(t),t,s)+laplace(i(t),t,s)/s+laplace(i(t),t,s)-i(0) = w/(w^2+s^2) |
Substituting i(0) as 0, and simplifying, we get laplace(i(t), t, s) = w/((w^2+s^2)*(s+1/s+1)). Solving that by inverse Laplace transform, we very easily get the complex expression for i(t) as follows:
(%i2) string(ilt(w/((w^2+s^2)*(s+1/s+1)), s, t));Is w zero or nonzero? |
n; /* Our input: Non-zero frequency */(%o2) w^2*sin(t*w)/(w^4-w^2+1)-(w^3-w)*cos(t*w)/(w^4-w^2+1)+%e^-(t/2)*(sin(sqrt(3)*t/2)*(-(w^3-w)/(w^4-w^2+1)-2*w/(w^4-w^2+1))/sqrt(3)+cos(sqrt(3)*t/2)*(w^3-w)/(w^4-w^2+1))(%i3) quit(); |