Check This New Sorting Algorithm Design

Sorting algorithms, which arrange the elements of a list in a certain order (either ascending or descending), are an important category in computer science. We can use sorting as a technique to reduce search complexity. Vast amounts of research has gone into this category of algorithms because of its importance, particularly in database algorithms.

Classification
Sorting algorithms are generally classified into different categories based on various factors like the number of comparisons, memory usage, recursion, etc. Existing sorting algorithms include the Selection, Bubble, Heap, Insertion, Quick, Merge, Counting, Bucket and Radix sort. All these different algorithms have some advantages and disadvantages.
The description of each of these algorithms is beyond the scope of this article.
The following gives a glimpse of how sorting works (with the Bubble sort):

Void bubble_sort(int arr[], int n) {
for(int pass=n-1;pass>=0;pass--)
// outer loop executed n times
{
for( int i=0; i<pass-1;i++)
// inner loop execute n times
{
if(arr[i]> arr[i+1])
{ // swapping the elements
Int temp=arr[i];
arr[i]= arr[i+1];
arr[i+1]=temp;
}
}
}
}

The above algorithm takes O(n2) time even in the best case.
Try optimising it so that we can skip some extra swaps by introducing an extra flag.
The following is optimised code of the above:

Void bubble_sort(int arr[], int n)
{
Int pass, I, temp, swapped=1;
for( pass=n-1; pass>=0&& swapped; pass--)
{
Swapped=0;
for( i=0; I<pass-1;i++)
{
If(arr[i]> arr[i+1])
{
temp=arr[i];
arr[i]=arr[i+1];
arr[i+1]=temp;
swapped=1;
}
}
}
}

This optimised version finally improves the time of the worst and best cases of the Bubble sort to O(n). This is called an optimisation of the code.

My new sorting algorithm
Recently, I developed a sorting algorithm that is able to sort any input (i.e., not ask for input restrictions) in O(n) time with O(n) Space Complexity. Though there are several sorting algorithms out there, which I mentioned earlier, some like Merge, Quick and Heap sort take O(nlogn) time, and some like Bubble, Selection and Insertion sort, take O( n2 ) time; but no algorithm takes O(n) time to throw up the result.
Of course, Counting, Radix and Bucket sort take O(n) time, but ask for input restrictions and finally cannot sort all the input given.
In this algorithm, we use a hash table implicitly to operate onto input elements, and only by doing two scans we are able to sort any kind of input (no input restriction) provided to us.

Implementation: How does it work?
Now, let us find a better solution to this problem. Since our objective is to sort any kind of input, what if we get the maximum elements and create the hash? So, create a maximum hash and initialise it with all zeros. For each of the input elements, go to the corresponding position and increment its count. Since we are using arrays, it takes constant time to reach any location.

Here is the main code implementation:

#include <stdio.h>
#include <conio.h>
#include <stdlib.h>

void main()
{
long int arr[]={62,4,8,423,43,4,432,44,23,2,55,12,3};
int n=sizeof(arr)/sizeof(arr[0]) ;
int i, j, k,l;
int min=arr[0];
int max=arr[0] ;
for(i=1;i<n;i++) // run for n times
{
if(arr[i]<min)
min=arr[i] ; // required for optimization
else if(arr[i]>max)
max=arr[i] ;
}
int *hash=(int*)calloc((max+1), sizeof(int)); //should be max+1

for(i=0;i<n;i++ )
{
hash[arr[i]]++; // storing the count of occurances of element
}
printf(“\n”);

for(i=0;i<max+1;i++) // loop to read the hash table...
{
if(hash[i]>0)
{
printf(“%d\t”, i) ; //print 1st time if the element has occured
}
j=hash[i]; /* this requires if the count of the element
is greater than one(if there is duplicates
element in the array) otherwise dupplicated element
will not be displayed more than once.*/
if(j==1 ||j==0)
continue;
while(j!=1)
{ // here we are printing till count not equal to 1
printf(“%d\t”, i) ;
j--;
}
}
getch();
}

The time complexity of the above algorithm is O(n) and with only two scans, we are able to arrive at the result. Its space complexity is O(n), as it requires extra auxiliary space (almost the maximum elements in an array) to get the result.

How is it better than other existing sorting algorithms?
Let’s check how this new algorithm compares with other existing sorting algorithms in terms of time complexity and speedup, flexibility and elegance of code.
I have already given you a glimpse of the Bubble sort and its optimisation. Now let’s take a look at the time complexity of existing algorithms:

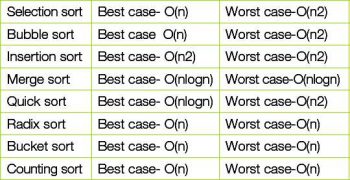
How the new sorting algorithm is better in terms of time-complexity and overhead
I am using rand(). The function rand() generates a pseudo-random integer number. This number will be in the range of 0 to RAND_MAX. The constant RAND_MAX is defined in the standard library (stdlib).

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
main()
{
int arr[10000],i,j,min,temp;
for(i=0;i<10000;i++)
{
arr[i]=rand()%10000;
}
//The MySort Agorithm
clock_t start,end;
start=clock();

min=arr[0];
int max=arr[0] ;
for(i=1;i<10000;i++)
{
if(arr[i]<min)
min=arr[i] ; // required for optimization
else if(arr[i]>max)
max=arr[i] ;
}
int *hash=(int*)calloc((max+1), sizeof(int)); //should be max+1

for(i=0;i<10000;i++ )
{
hash[arr[i]]++; // storing the count of occurances of elements
}
printf(“\n”);
end=clock();
double extime=(double) (end-start)/CLOCKS_PER_SEC;
printf(“\n\tExecution time for the MySort Algorithm is %f seconds\n “,extime);
for(i=0;i<10000;i++)
{
arr[i]=rand()%10000;
}
clock_t start1,end1;
start1=clock();
// The Selection Sort
for(i=0;i<10000;i++)
{
min=i;
for(j=i+1;j<10000;j++)
{
if(arr[min]>arr[j])
{
min=j;
}
}
temp=arr[min];
arr[min]=arr[i];
arr[i]=temp;
}
end1=clock();
double extime1=(double) (end1-start1)/CLOCKS_PER_SEC;
printf(“\n”);
printf(“\tExecution time for the selection sort is %f seconds\n \n”,extime1);
if(extime1<extime)
printf(“\tSelection sort is faster than MySort Algorithm by %f seconds\n\n”,extime- extime1);
else if(extime1>extime)
printf(“\tMysort Algorithm is faster than Selectionsort by %f seconds\n\n”,extime1-extime);
else
printf(“\tBoth algo has same execution time\n\n”);
}

How is this sorting algorithm better than Merge sort and Quick sort algorithms in terms of both time complexity and overhead spent?

Both Merge sort [O(nlogn)] and Quick sort [O(nlogn)-best case] use recursion to sort the input; also, the running time of Quick sort in the worst case is O(n2). There are always certain overheads involved while calling a function. Time has to be spent on passing values, passing control, returning values and returning control. Recursion takes a lot of stack space. Every time the function calls itself, memory has to be allocated, and also recursion is not good for production code.
In the new sorting algorithm, we are getting rid of all issues—the recursion, the time and the overhead. In comparison with the Merge and Quick sort, we are almost cutting the time by logn and making the new algorithm to run in O(n) time.
It may happen that when you try to compare the execution time of Merge and Quick sort and the new sorting algorithm, they may give the same or equal execution time based on the above method by introducing clock, but again, you cannot measure the accurate running time by doing so.
I am providing a Merge sort algorithm here, so that you can refer to and trace the difference in both codes, and see how many recursions and function calls are involved:

/* Function to merge the two haves arr[l..m] and arr[m+1..r] of array arr[] */
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;

/* create temp arrays */
int L[n1], R[n2];

/* Copy data to temp arrays L[] and R[] */
for(i = 0; i < n1; i++)
L[i] = arr[l + i];
for(j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
/* Merge the temp arrays back into arr[l..r]*/
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
/* Copy the remaining elements of L[], if there are any */
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
/* Copy the remaining elements of R[], if there are any */
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
/* l is for left index and r is right index of the sub-array
of arr to be sorted */
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
int m = l+(r-l)/2;
//Same as (l+r)/2, but avoids overflow for large l and h
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}

Finally, as every algorithm has some pros and cons according to the input provided, some of the advantages and disadvantages of this new sorting algorithm are listed here.

Advantages

• Time efficient about O(n) in even the worst case, and has sorting flexibility
• Elegant and lucid code that is easy to understand
• Requires only two scans to get the result, and it is free from recursion and extra overhead
• Is an advantage in many problems that use sorting as pre-processing to arrive at the result

Disadvantages

• It requires extra space as per input provided
• Wastes much of the space if the input is short and has a large number at any point, e.g., {5, 1, 11, 395, 159, 64, 9,}, though situations like this rarely occur

Applications of this sorting algorithm
There are several applications and uses that require sorting as pre-processing before doing real computation to get the result, which takes O(nlogn) as the total running time. This particular problem can be decreased to a time of O(n) with the help of this new sorting algorithm. Some examples can be:

• Finding the majority element
• Finding the triplet in an array
• Finding two elements whose sum is closest to zero.